In the last few years, literary studies have experienced what we could call the rise of quantitative evidence. This had happened before of course, without producing lasting effects, but this time it is probably going to be different, because this time we have digital databases and automated data retrieval. As a recent article in Science on ‘Culturomics’ made clear, the width of the corpus and the speed of the search have increased beyond all expectations: today, we can replicate in a few minutes investigations that took a giant like Leo Spitzer months and years of work.footnote1 When it comes to phenomena of language and style, we can do things that previous generations could only dream of.
When it comes to language and style. But if you work on novels or plays, style is only part of the picture. What about plot—how can that be quantified? This paper is the beginning of an answer, and the beginning of the beginning is network theory. This is a theory that studies connections within large groups of objects: the objects can be just about anything—banks, neurons, film actors, research papers, friends . . .—and are usually called nodes or vertices; their connections are usually called edges; and the analysis of how vertices are linked by edges has revealed many unexpected features of large systems, the most famous one being the so-called ‘small-world’ property, or ‘six degrees of separation’: the uncanny rapidity with which one can reach any vertex in the network from any other vertex. The theory proper requires a level of mathematical intelligence which I unfortunately lack; and it typically uses vast quantities of data which will also be missing from my paper. But this is only the first in a series of studies we’re doing at the Stanford Literary Lab; and then, even at this early stage, a few things emerge.
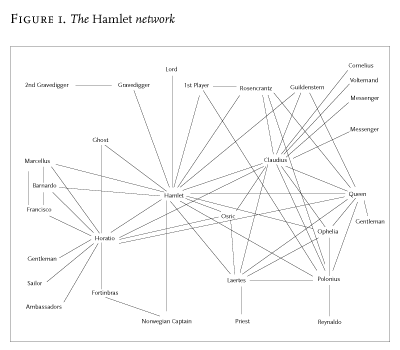
A network is made of vertices and edges; a plot, of characters and actions: characters will be the vertices of the network, interactions the edges, and this is what the Hamlet network looks like: Figure 1.footnote2 There are some questionable decisions here, mostly about The Murder of Gonzago, but, basically, two characters are linked if some words have passed between them: an interaction is a speech act. This is not the only way to do things, the authors of a previous paper on Shakespeare had linked characters if they had speaking parts during the same scene, even if they did not address each other: so, for instance, for them the Queen and Osric are linked (because they both have speaking parts, and are on stage together in the last scene of the play), whereas here they are not, because they don’t speak to each other.footnote3 My network uses explicit connections, theirs adds implicit ones, and is obviously denser, because it has all of my edges plus some; both are plausible, and both have at least two flaws. First, the edges are not ‘weighted’: when Claudius tells Horatio in the graveyard scene, ‘I pray thee, good Horatio, wait upon him’, these eight words have in this figure exactly the same value as the four thousand words exchanged between Hamlet and Horatio. This can’t be right. And then, the edges have no ‘direction’: when Horatio addresses the Ghost in the opening scene, his words place an edge between them, but of course that the Ghost would not reply and would speak only to Hamlet is important, and should be made visible.footnote4 But, I just couldn’t find a non-clumsy way to visualize weight and direction; and turning to already-existing software didn’t help, as its results are often completely unreadable. So, the networks in this study were all made by hand, with the very simple aim of maximizing visibility by minimizing overlap. This is not a long-term solution, of course, but these are small networks, in which intuition can still play a role; they’re like the childhood of network theory for literature; a brief happiness, before the stern adulthood of statistics.
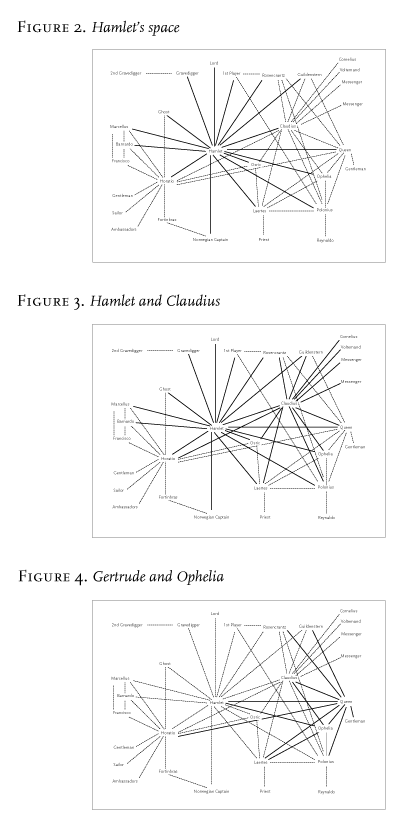
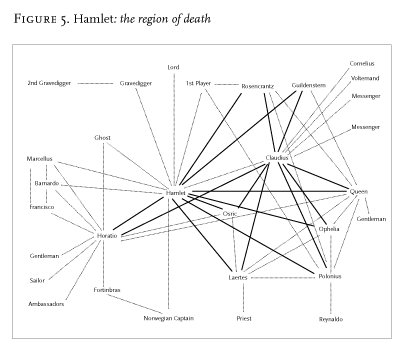
Anyway. Four hours of action, that become this. Time turned into space: a character-system arising out of many character-spaces, to use Alex Woloch’s concepts in The One vs the Many. Hamlet’s space, Figure 2: in bold, all the direct links between him and other characters; Hamlet and Claudius, Figure 3: see how much of the network they capture, between the two of them. Ophelia and Gertrude, Figure 4: the much smaller space of the two women in the play. And so on. But before analysing spaces in detail, why use networks to think about plot to begin with? What do we gain, by turning time into space? First of all, this: when we watch a play, we are always in the present: what is on stage, is; and then it disappears. Here, nothing ever disappears. What is done, cannot be undone. Once the Ghost shows up at Elsinore things change forever, whether he is on scene or not, because he is never not there in the network. The past becomes past, yes, but it never disappears from our perception of the plot.
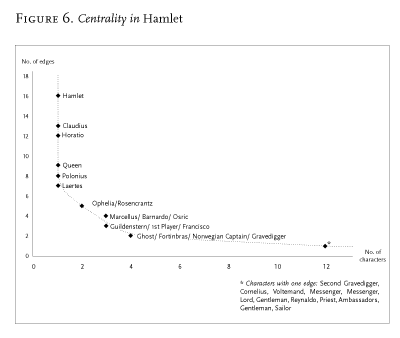
Making the past just as visible as the present: that is one major change introduced by the use of networks. Then, they make visible specific ‘regions’ within the plot as a whole: sub-systems, that share some significant property. Take the characters who are connected to both Claudius and Hamlet in Figure 5: except for Osric and Horatio, whose link to Claudius is however extremely tenuous, they are all killed. Killed by whom, is not always easy to say: Polonius is killed by Hamlet, for instance—but Hamlet has no idea that it is Polonius he is stabbing behind the arras; Gertrude is killed by Claudius—but with poison prepared for Hamlet, not for her; Hamlet is killed by Laertes, with Claudius’s help, while Laertes himself, like Rosencrantz and Guildenstern before him, are all killed by Hamlet, but with Claudius’s weapons. Individual agency is muddled; what is truly deadly, is the characters’ position in the network, chained to the warring poles of king and prince. Outside of that bold region, no one dies in Hamlet. The tragedy, is all there.
Third consequence of this approach: once you make a network of a play, you stop working on the play proper, and work on a model instead. You reduce the text to characters and interactions, abstract them from everything else, and this process of reduction and abstraction makes the model obviously much less than the original object—just think of this: I am discussing Hamlet, and saying nothing about Shakespeare’s words—but also, in another sense, much more than it, because a model allows you to see the underlying structures of a complex object. It’s like an X-ray: suddenly, you see the region of death of Figure 5, which is otherwise hidden by the very richness of the play. Or take the protagonist. When discussing this figure, literary theory usually turns to concepts of ‘consciousness’ and ‘interiority’—even Woloch’s structural study takes this path. When a group of researchers applied network theory to the Marvel comics series, however, their view of the protagonist made no reference to interiority; the protagonist was simply ‘the character that minimized the sum of the distances to all other vertices’;footnote5 in other words, the centre of the network. In their case, it was a character called Captain America; in ours, it is Hamlet. One degree of separation from 16 of the characters; two degrees from the others; average distance from all vertices in the network, 1.45. And if we visualize these results in the form of a scatter-plot, Figure 6 (below), we find the power-law distribution that is characteristic of all networks: very few characters with many edges on the left, and very many characters with just one or two edges on the right. The result is the same if we add all the characters from Macbeth, Lear and Othello. Power-law is the opposite of a Gaussian curve: there is no central tendency in the distribution, no ‘average’; that is to say, there is no ‘typical’ vertex in the network, and no typical character in the plays. So, speaking of Shakespeare’s characters ‘in general’ is wrong, at least in the tragedies, because these characters-in-general don’t exist: all there is, is this curve leading from one extreme to the other without any clear solution of continuity. And the same applies to the binaries with which we usually think about character: protagonist versus minor characters, or ‘round’ versus ‘flat’: nothing in the distribution supports these dichotomies; what it asks for, rather, is a radical reconceptualization of characters and of their hierarchy.
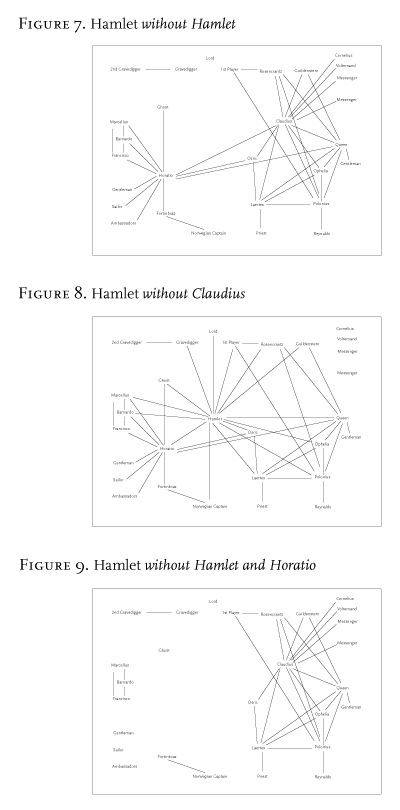
What is done is never undone; the plot as a system of regions; the hierarchy of centrality that exists among characters; finally—and it is the most important thing of all, but also the most difficult—one can intervene on a model; make experiments. Take the protagonist again. For literary critics, this figure is important because it is a very meaning-ful part of the text; there is always a lot to be said about it; we would never think of discussing Hamlet—without Hamlet. But this is exactly what network theory tempts us to do: take the Hamlet-network, and remove Hamlet, to see what happens: Figure 7. And what happens is that the network almost splits in half: between the court on the right, and the region that includes the Ghost and Fortinbras on the left all that remains are the three edges linking Horatio to Claudius, Gertrude and Osric: a few dozen words. If we used the first Quarto, the breakdown would be even more dramatic.