In Capital Volume One Marx set out his theory of value and exploitation and showed, through his concept of the value of labour power, how ‘freedom’ of exchange is quite compatible with exploitation and the existence of surplus value. His argument was both strengthened and simplified by the assumption that commodities exchange at value. In Volume Three Marx turned to the more detailed question of how the profit rate and prices are determined when the organic composition of capital differs between industries and consequently commodities do not exchange at value. He was anxious to stress the idea that fundamentally profits and prices are just ‘transformed’ value quantities, so that the essence of the Volume One argument is unaffected by the Volume Three complications. Over the last 15 years or so, academic economics has generated a considerable discussion of questions which bear directly on Marx’s treatment of the relations between wages, profits, values and prices: relations which are clearly of importance for Marxist analyses of many issues in political economy.footnote1 The purpose of this article is to set out, by means of a simple numerical example,
Marx normally described the economy in terms of value quantities, such as C (constant capital), V (variable capital), S (surplus value) and W (total value of gross output). These value quantities, however, were determined by two different things which Marx assumed to be given, in a given capitalist economy at a given point in time. On the one hand they depended on the existing conditions of production, both technical and social, which defined the relations between inputs and outputs in the productive process. On the other hand they depended on the division of the net product between workers and capitalists in that society. We shall turn to the value quantity representation of the economy below but, for reasons which will emerge later, we start by describing the economy in physical terms.
Consider a very simple economy with three industries. One industry produces the means of production, let us call it iron, one produces gold and the third produces a necessary consumption good, say corn. In each industry the production process uses only labour and iron as inputs; the amount of iron used per unit of labour varies between the industries, but whichever industry iron is used in it is completely used up in one year. Thus there is no fixed capital.
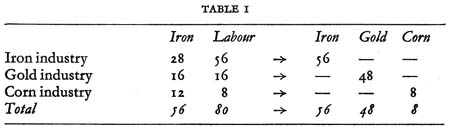
Table 1 shows the physical inputs to, and physical outputs from each industry, with inputs to the left of the arrows and outputs to the right. (The argument does not, of course, depend on the particular figures given here). The final row shows the physical inputs and outputs for the economy as a whole.
Thus the first row shows that 56 units of labour, working with 28 units of iron, produce 56 units of iron; the second shows that 16 units of labour, working with 16 units of iron, produce 48 units of gold; while the third shows that eight units of labour, working with 12 units of iron, produce eight units of corn. (The physical units to which we refer
By the value of a commodity, Marx meant that quantity of labour socially necessary for the production of that commodity. This value, or quantity of labour, includes, of course, not only the labour directly used in the production of the commodity but also the labour used indirectly in its production or, in other words, the labour required to produce the means of production used up in the direct labour process. This latter labour, in turn, includes the labour directly used in the production of these means of production and the labour required to produce the means of production used in making them. Continuing this process backwards through time (always ‘resolving’ the labour embodied in means of production into direct labour and further labour embodied in means of production), we then see the value of a commodity as made up of a sequence of expenditures of labour spread out through time. If we let the values of a unit of iron, gold and corn be li, lg and lc respectively, then we can determine these values from the data of Table 1.
To determine li, consider the first row of Table 1. The total value of output in the iron industry is clearly 56 li. This is made up of 56 units of direct labout time plus the indirect labour required to produce 28 units of iron. This latter quantity of labour can be found by simply halving all the quantities footnote3 in the first row of Table 1; it will consist of 28 units of direct labour plus the labour required to produce 14 units of iron. This last quantity of labour can now be found, in the same way, by taking one quarter of the quantities in the first row of Table 1; and so on. As we repeat this process without limit we find that